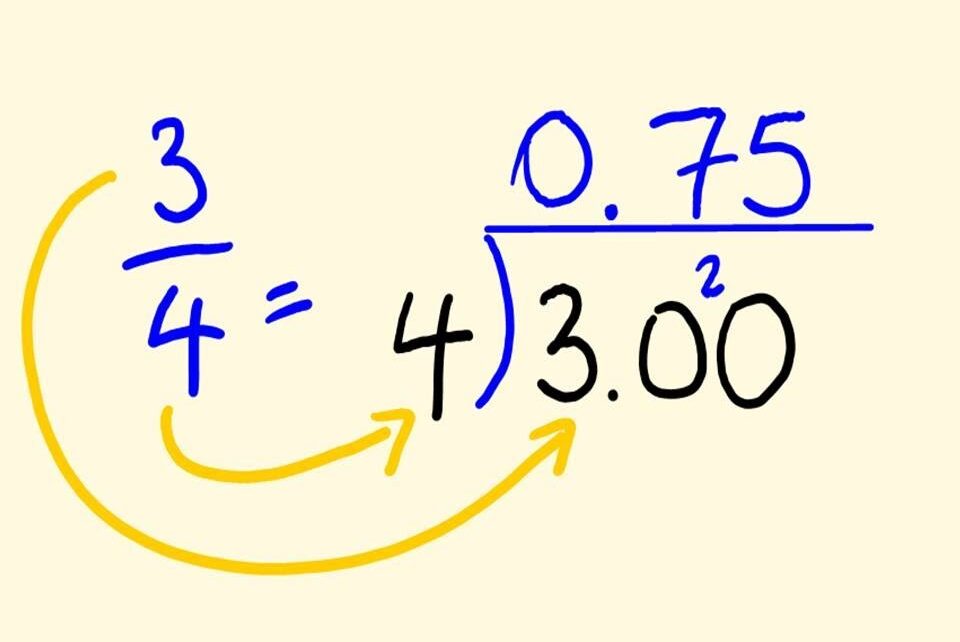The term fraction can also be referred to as a part or a piece of a bigger number. The ‘/’ sign, as in a/b, is used to symbolise it. For example, 5/7 is a fraction wherein the top part is known as the numerator and the lower part of the fraction is known as the denominator.
Consider this, if you take half a portion of any pizza and split it into 2 equal pieces, each piece will represent a quarter of the entire pizza.
1/2÷2 which is equal to ¼
This is known as Dividing Fractions. The division is the process of dividing a thing into ‘n’ equal pieces, where ‘n’ can be any number. Division can be performed using whole numbers, integers, fractions, or decimals. In this article, we are going to know how to convert fraction to decimal.
Let’s learn it with an example:
Convert the fraction ⅕ into a decimal?
Step 1: Put a 0 after 1 in the numerator.
Step 2: It would look like this – 10/5, but this will automatically add a decimal to the solution.
Step 3: 10/5 = 0.2
Step 4: ⅕ gets converted to 0.2
Dividing Fractions
Converting decimals to fractions is a frequent mathematical process. Furthermore, in order to do so, students should first understand the foundations of division. It will be very easy to convert decimals to fractions as well as fractions to decimals, Let’s look at how to convert any decimal to a fraction.
Example1: 0.6 is a given decimal number. Convert the specified decimal to a fraction.
Solution: The First stage is to evaluate the place value of the numbers following the decimal place in each given question.
The number 0.6 is alternatively written as 0.60, which indicates, the decimal point (.) is in the tenth position.
6/10 = 3/5 which will be the fractional form of the decimal number 0.6
Example 2: 0.22 is a given decimal. Convert 0.22 into a fraction.
Solution: The First stage is to evaluate the place value of the numbers following the decimal place in each given question.
The decimal number 0.22 can also be written as 0.220 which indicates that the decimal point (.) is in the 100th position.
So in terms of fractions, we can represent the decimal 0.220 as 22/100. On reducing to simpler terms we get 11/50, we cannot reduce it to simpler terms.
Steps for Dividing Fractions
- Leave the very first portion alone.
- Reciprocate the other fraction (that we wish to divide) in the other direction, i.e. inverted.
- Now the very first step is to multiply the first fraction by its reciprocal.
- Reduce the fraction to it’s lowest terms if necessary.
Facts About Fractions
- The fraction’s numerator indicates how many equal chunks of the set are taken. (For example, if you cut an apple into 6 slices and take 4, the numerator is 4.)
- The total number of equal components in the collection is shown in the denominator. (For example, if an apple had a total of seven slices, the fraction’s denominator would be 7).
Dividing Fractions in Daily Life
You would be wondering where dividing fractions come in use in daily life, let us see:
- When we go shopping and need to compute the price of a product after a sale, we must know how to divide fractions.
- Whenever we prepare anything or make a meal, we need a precise amount of each ingredient, and here is where we need to understand how to divide fractions.
- Dining with someone, have you ever dined out with pals? We must also utilize fractions to divide the cost in this case.
- Shopping for Groceries, when we view invoices for shopping, sales tax, and coupons, we see that they all employ fractions.
- When it comes to knowing the purity of the item.
- Time, time is sometimes measured in fractions such as a quarter of an hour or a half an hour.
Refer to the Cuemath website for learning more skills in maths with two-sided and fun interactive sessions.